HW7 Solution

Here’s a .do file you may use

• Key Points:

  • Code that replicates the images is correct

  • But its a little nuanced:

    • If your machine runs anything before Stata 18, the format will be correct

    • So you have to look for the conditional if c(version) statament

    • Less reason to be vigilant if you’re running Stata 18

  • Replicating the image but without the “Classic” Stata look is ok

    • But some points have to be dropped based on the Rubric

  • The core idea of this class is that Stata code should anticipate variation in operating systems (c(os)), filepaths (/ vs. \), Stata versions (c(version)), and so much more

    • A script that runs on one computer may not successfully run on another

    • Scripts that embrace such ambiguity must be awareded credit as per the rubric

    • Conditional statements that creatively invoke system or user-defined macros are the best evidence

      • e.g. if _rc !=0 {

global repo https://github.com/jhustata/basic/raw/main/

//This allows you to recreate the exact figures and color schemes
//You'll lose 1pt overall if you're color schemes are the default from Stata 18
if c(version)>17 { //tip 4 hw3
    set scheme s2color
}
else { //stcolor is default in v18
    di "you're good to go!"
}

(late assignments will not be accepted for graduating students)

Write a .do file which performs the tasks described below. Your .do file should be called hw7.lastname.firstname.do. Do not submit your log files as part of the assignment.

Codebook

Variable	Description	Values
tx.dta
ctr_id	Center ID	Integer
transplant_date	Date of transplant	Date
prev_ki	Recipient has history of previous kidney transplant?	Binary (1=Yes/0=No)
age	Recipient’s age	Integer
bmi	Recipient’s BMI	Numeric

Question 1

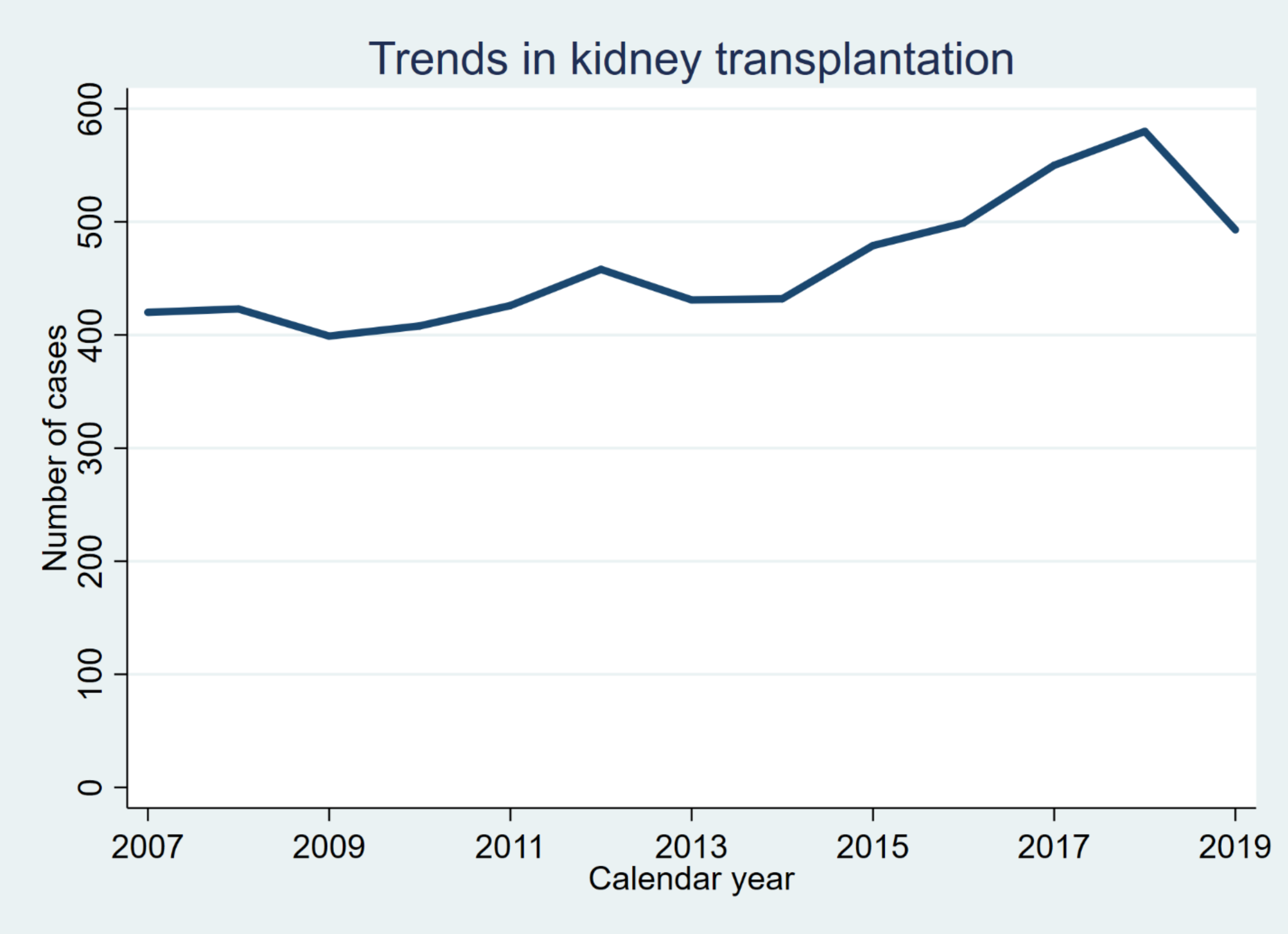
Clear the memory and load tx.dta. Drop all observations with missing values on transplant_date. Reproduce the following graph as precisely as possible.

This graph shows a line plot of the number of cases performed in each calendar year. Be mindful about the thickness of the line, the main title, and the axis labels and titles.

use ${repo}tx, clear
gen year = year(transplant_date)

Save the graph as q1_[yourname].png

Question 2

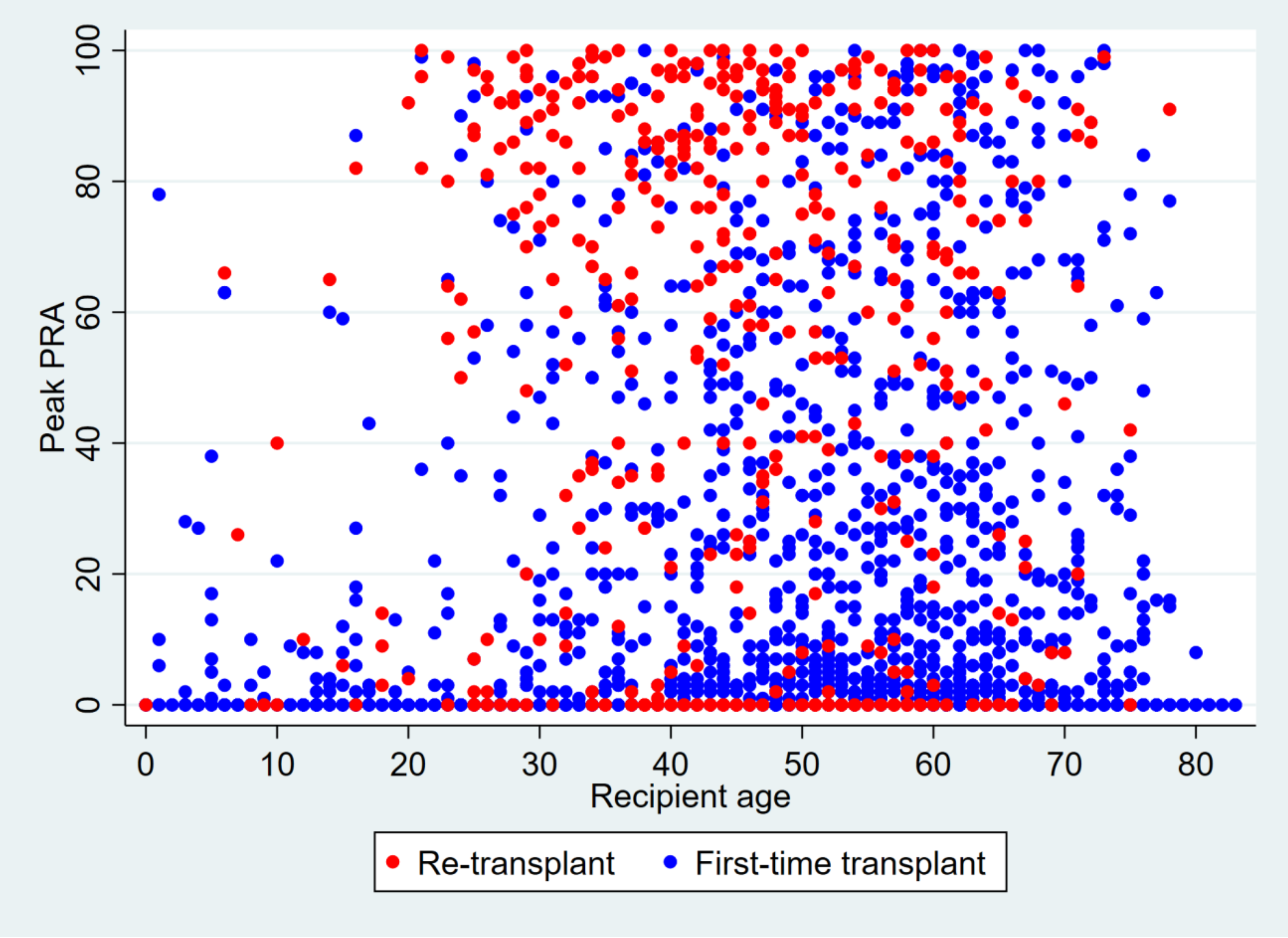
Clear the memory and load tx.dta. Drop all observations with missing values on peak_pra. Reproduce the following graph as precisely as possible.

This graph shows a scatter plot of peak_pra and age, stratified by prev_ki. Observations with prev_ki == 1 are shown in red. Be mindful about the color (“blue” and “red” in Stata color codes) and size of the markers, the axis titles, and the legend.

Save the graph as q2 _[yourname].png

Question 3

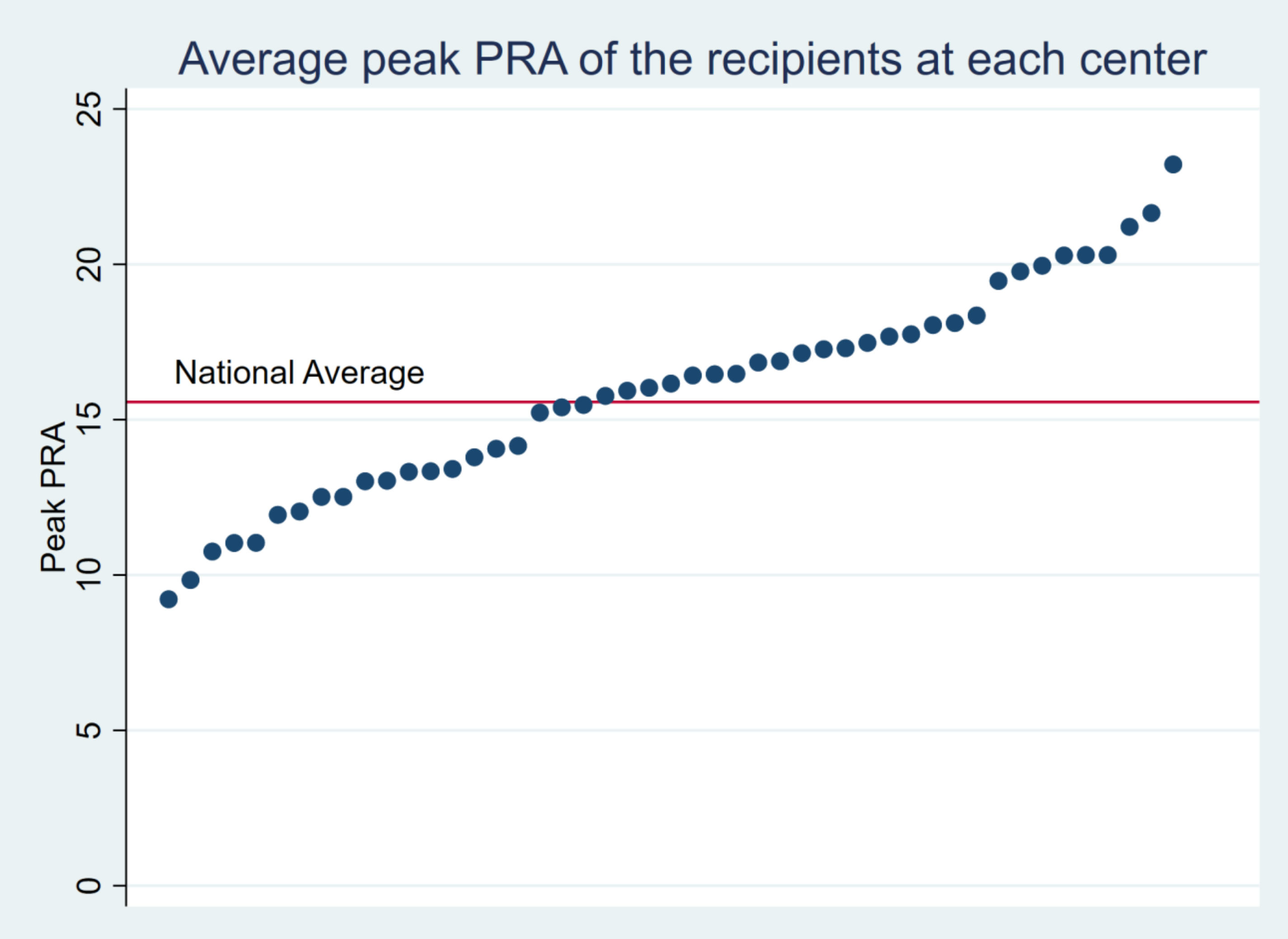
Clear the memory and load tx.dta. Drop all observations with missing values for peak_pra. Reproduce the following graph as precisely as possible.

Calculate the average of peak_pra at each transplant center (ctr_id). Display the average value of peak_pra after sorting. The location of the text label “National Average” can be hardcoded (i.e. manually specify the location; about x=7 and y=17). Other markers and lines should NOT be hardcoded and should be derived by your script using the dataset.

Save the graph as q3 _[yourname].png

Additional Credit (Maximum \(+5\))

Use the Extra credit challenge DropBox

Write a program called sampmean to plot random data drawn from a normal distribution. sampmean takes a list of numbers representing different sample sizes. It also takes (optionally) a mean and standard deviation for the normal distribution. If we run

sampmean, at(5 20 100 1000) mean(20)

We get a graph like this:

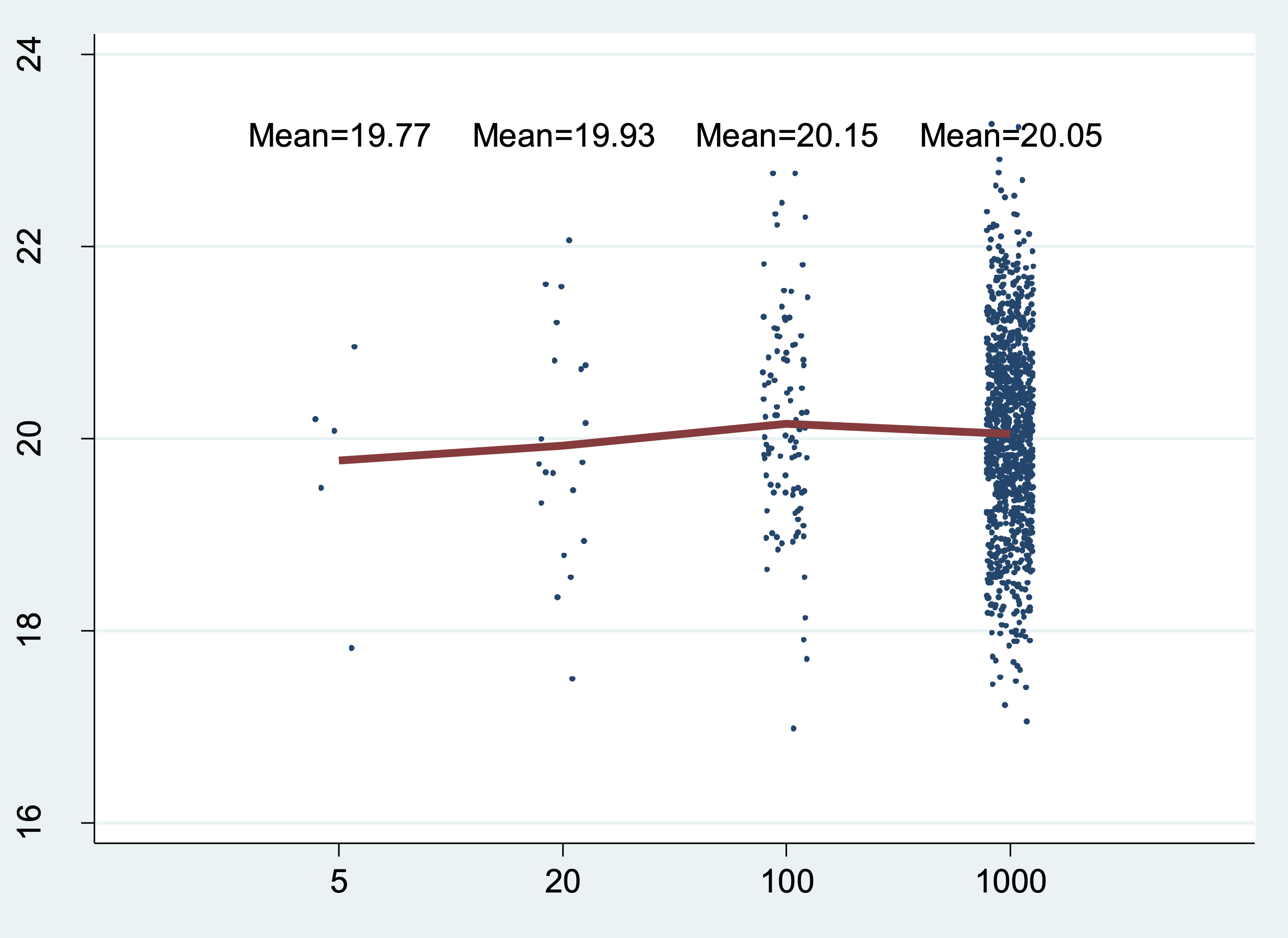
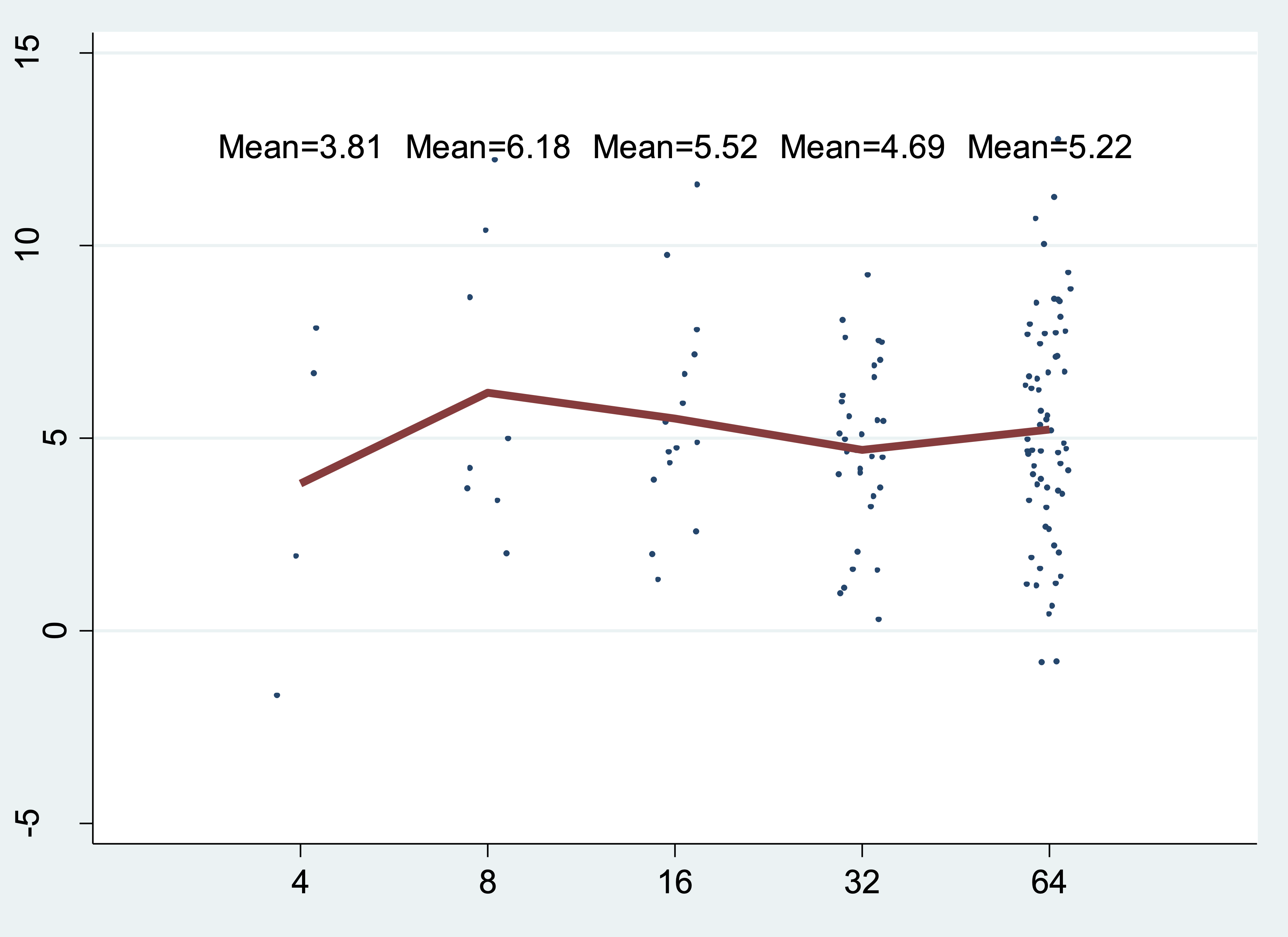
In this example, the program generates four sets of normally distributed random numbers (one set of 5 numbers, one set of 20, one set of 100, and one set of 1000) and calculates the mean for each set. It also plots each randomly generated number (as points) and the group mean (as a red line). The group mean also appears above each group as text.

Here are some more examples. The exact output will depend on the random number seed you use.

sampmean, at (4 8 16 32 64) mean(5) sd(3)

sampmean, at(100 200 300) mean(5) sd(2) uniform

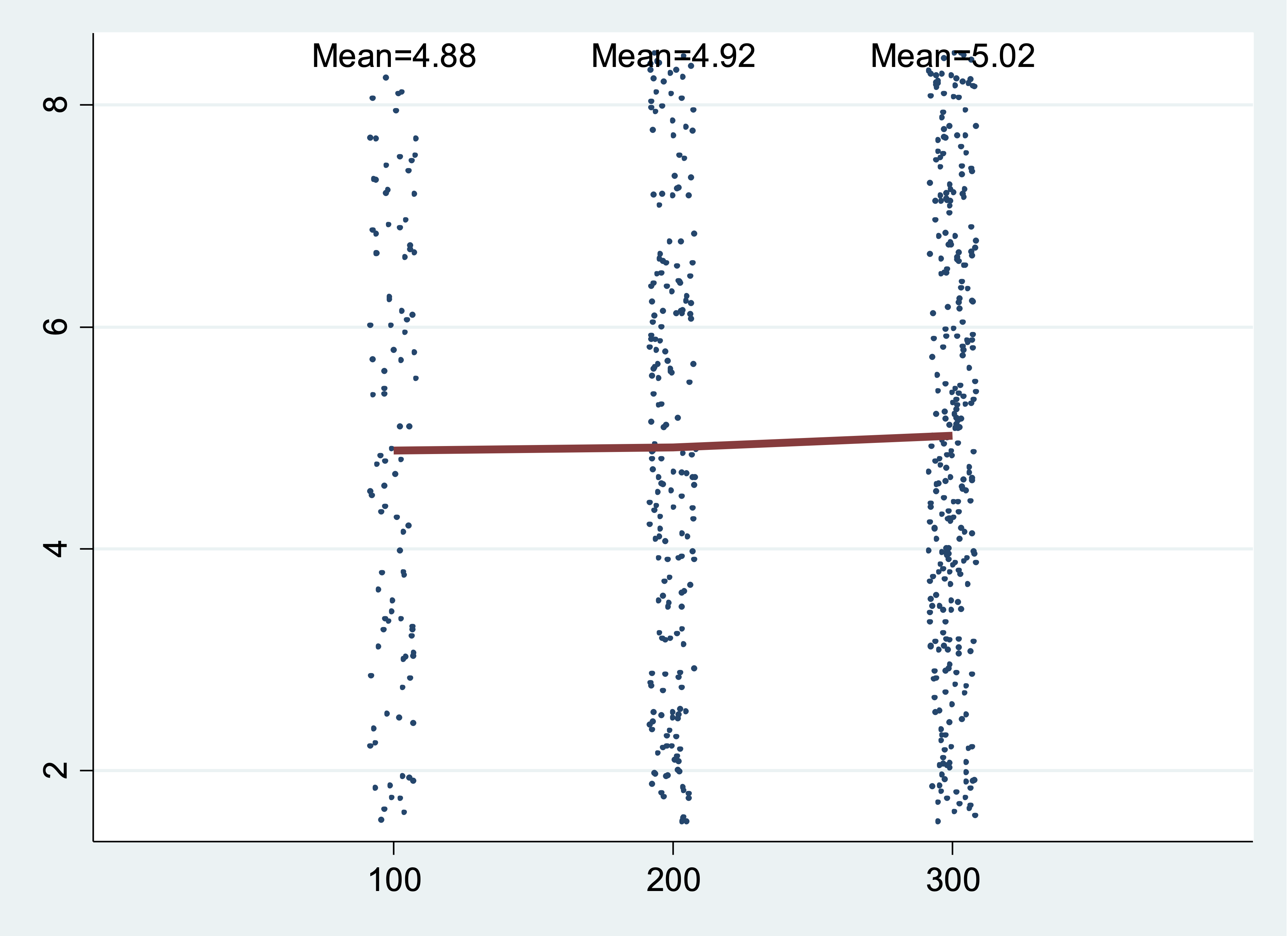
In the last example, the distribution is a uniform distribution instead of a normal distribution.

Hints:

• You can use the keyword numlist (for a list of numbers) just as you do with a varlist (list of variables)

• The uniform distribution from 0 to 1 has mean 0.5 and standard deviation sqrt(1/12).

Note: this problem is pretty hard! We expect that few people will solve the whole thing, but we will give partial credit for a partial (working) solution. If your program only works partly, then explain in the comments, like this: